基于并聯電抗器線路行波的研究

      摘 要：隨著電力系統的發展，一些特殊結構的輸電線路如帶并聯電抗器線路應用日益廣泛，當行波差動保護應用于這些特殊線路時會面臨一些新的問題。為此，論文基于這種特殊線路的模型研究推導出合理準確的行波差流定義式，同時結合所提的實用方案及技術，實現了行波差動保護在這種特殊線路中的應用。

　　關鍵詞：并聯電抗器；行波；差動保護
　　
　　引 言
　　隨著電力系統的發展，電網規模的擴大，為限制線路過電壓、提高線路輸送能力、增強系統穩定性或節省投資等，一些特殊拓撲結構的輸電線路如帶并聯電抗器線路、T接線路、帶串補線路、同桿并架雙回線路等在國內外超(特)高壓電力系統中應用日益增多。行波差動保護由于能夠從理論上消除電容電流的影響，因而在超(特)高壓輸電長線保護中具有很大的優勢。但當行波差動保護應用于上述特殊的輸電線路時會面臨一些新的問題，如在這些裝置或T節點發生行波的反射和折射，或回路間存在零序耦合等，因而適合于普通雙端線路的方案在此不能直接應用，因此有必要對此展開深入的研究，探求適合于這些特殊線路的行波差動保護方案。本文針對行波差動保護在帶并聯電抗器線路應用時存在的問題，基于其模型結構經研究推導給出了合理準確的行波差流表達式，實現了行波差動保護在這種特殊線路中的應用。
　　
　　一、行波的基本特性
　　圖示單相分布參數線路MN，設單位長度電阻為R，電感為L，電導為G，電容為C。按照圖示的電壓和電流參考方向，可得均勻分布參數線路電壓電流關系的偏微分方程如下：行波差動保護應用于帶并聯電抗器線路時，同樣會受到線路模型誤差、插值計算誤差、波速不一致性等因素的影響，正常運行或區外故障時也會產生一定的不平衡差流，若通過提高動作電流門檻來防止保護誤動，勢必會影響區內高阻故障時的靈敏度。
　　
　　為此對于帶并聯電抗器線路上式行波制動電流定義為與傳統的電流差動保護相比，行波差動保護只是在差流形成上有所區別，傳統電流差動保護的有關實用技術完全可以應用于行波差動保護中。從傳統電流差動保護電容電流補償措施的角度出發，行波差動保護通過引入傳輸時間τ、波阻抗ZC以及兩端的電壓量，能完全補償線路電容電流，理論上不必考慮電容電流引起的不平衡分量，因而Idz可顯著降低。對于實際三相輸電線路，同樣可采用模變換解耦方法得到各相的行波差流和制動電流從而構成分相差動保護，實現選相跳閘。
　　
   二、帶并聯電抗器線路的行波差動保護
　　特/超高壓輸電長線中為吸收高壓電網過剩的無功功率，防止過電壓，同時對線路進行參數補償，通常需要裝設并聯電抗器。并聯電抗器可能裝設在線路兩側，也可能裝設在線路中間或在線路兩側和中點均裝設。行波傳輸到并聯電抗器時，會發生反射和折射，式(5)的判據將會產生不平衡差流，抬高動作門檻值，影響行波差動保護的靈敏度，因此必須要采取措施消除并聯電抗器的影響。
　　
　　圖中，設,,MNKuuu為線路M側、N側和中點的電壓，線路電流及其正方向如圖2所示，MNKLLL分別為兩側及中點并聯電抗器的電感。先考慮線路中間沒有并聯電抗器的情況，即假設圖2中的KL→∞，此時線路M′-N′仍為普通線路，故可得行波差流為行波差動保護是基于無損線路的，實際線路存在電阻分量，因而正常運行或區外故障時會存在一定的不平衡差流。另外，對于帶并聯電抗器線路，由于式(15)~(17)采用差分代替微分，存在數值計算誤差，也會產生不平衡差流。若通過提高差動保護的最小動作電流dzI來防止保護誤動，勢必會影響區內高阻故障時的靈敏度。為此，參照傳統電流差動保護的方法，在門檻值dzI的基礎上引入電流行波制動量。
　　
　　三、仿真分析
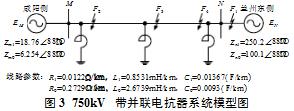
　　本文利用EMTP電磁暫態仿真程序，對圖3所示西北電網蘭州東−咸陽750kV試驗線路進行仿真計算。線路全長497km，咸陽側和蘭州東側各裝有1臺3×90Mvar和1臺3×100Mvar的并聯電抗器，線路中點裝設2臺3×100 Mvar的并聯電抗器，具體系統和線路參數見圖3。由參數計算得波阻抗為CZ=250Ω，0CZ=550Ω，線路M-N上的行波傳輸時間為τ=1.7ms, 0τ=2.5ms。M側為本側，N側為對側。由于目前2M速率光纖通道已經普遍應用，電流電壓每周波采樣24點，對側傳送的數據進行插值處理后再調用。
　　
　　在常規電流差動保護中，線路空充時不平衡差流最大，因此可先考察線路空充時行波差動保護的特性。將圖3中的N側三相斷開，M側合閘，所得的行波差流如圖4所示(圖中只畫出了較嚴重的先合相a相波形，所得結論適用于其它兩相)。從這些波形中可以看到，雖然在線路空充(或區外故障)時，理論上不會產生行波差流，但由于數值計算和線路參數模型(忽略線路電阻)誤差等原因，實際應用時存在不平衡行波差流。瞬時值行波差流中的暫態不平衡量最大值達到2.13kA，遠遠大于穩態不平衡量，且主要由高次諧波組成，說明上述誤差對高次諧波比較敏感。采取半波富氏或全波富氏算法后，行波差流大為降低(例如采用全波富氏算法后的最大值為0.16kA，只有瞬時值行波的7.5%)，所以在實際應用中采取適當的濾波措施是必要的，可以顯著降低行波差動保護的動作門檻。

　　雖然全波富氏算法的數據窗長度比半波富氏算法大1倍，但最大行波差流只有半波富氏算法的0.45(0.16/0.356)。差動保護在區內故障時不必等到算法數據窗滿后才投入，由于采取全波富氏算法后，保護的動作門檻比半波富氏算法降低1倍，區內故障時并不會影響動作速度，故本文采用全波富氏算法。顯然，在采用全波富氏算法后，行波差動保護對裝置采樣率的要求并不比常規差動保護高，完全可以在現有技術條件下實現。
　　
　　從圖4(d)可看到，線路空充后行波差流與制動電流比值m很小，最大值只有0.033。若采用式(22)的比例制動特性，比例制動系數k可以取得很低，不會影響區內故障時的靈敏度。順便指出，對于常規差動保護，在線路空充時只有一側有電流，比例制動特性不能發揮作用，但是行波差動保護由于引入了電壓量，故在線路空充時仍具有很強的制動作用。 圖5為區外F1處發生AG金屬性故障時(經全波富氏算法的)行波差流和m值曲線。故障前行波差流很小，約0.012kA，比值m≈0.004。故障后的暫態過程中，行波差流的最大值約0.144kA，m最大值約為0.023。暫態過程結束后，穩態的行波差流和比值m分別約為0.065kA和 0.009。
　　
　　對照圖4可以看到，正常運行時行波差流和比值m均最小，而線路空充時行波差流和比值m均最大。對于區外多相故障也進行的仿真計算，證明上面的結論仍然成立。因此，對于式(22)的具有比例制動特性的行波差動保護判據，最小動作差流Idz可以按躲過正常運行的不平衡差流整定，以有效地降低動作門檻，提高保護的靈敏度；比例制動系數k則應該按照躲過線路空充時的最大m值整定，考慮一定的裕度，建議取k=0.1~0.15。
　　
　　圖6為線路F4點發生a相400Ω接地故障時(經全波富氏算法)的行波差流和m值曲線，故障前的行波差流和比值m值與圖5相同。故障后行波差流和比值m的穩態值分別約為1.83kA和0.613。由圖6知，故障后行波差流和比值m上升很快，且幾乎是單調上升的。故障后2ms差流達到故障前差流17倍，此時對應的m值為0.12。由此可見，即使采用了全波富氏這樣的長窗算法，行波差動保護在高阻故障時仍具有非常快的動作速度。

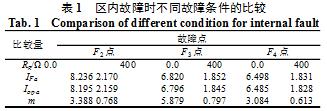
    表1列出了線路區內AG故障時不同故障點、不同過渡電阻條件下故障點電流、行波差流及m值的比較。可見行波差流opaI⋅與故障點電流FaI非常接近，即判據的行波差流值能時時反映故障點電流值。此外，在末端高阻接地故障時，行波差流與制動電流之比m取得最小值minm=0.613，遠大于區外故障、線路空充時的m值。
　　
    四、結論
　　針對帶并聯電抗器的特/超高壓輸電長線，本文給出了一種新的行波差流表達式，并據此提出了一種具有輕微比例制動特性的行波差動保護實用方案，理論和仿真計算表明：
　　（1）采用本文定義的行波差流表達式后，線路正常時的不平衡動作電流值大為降低。
　　（2）區外故障、線路空充時有較大的暫態不平衡電流，采用具有比例制動特性的行波差動保護能降低動作門檻值，提高保護的靈敏度。
　　（3）區內故障時，行波差流和m值迅速增大，且m均大于整定的k值，保護能快速動作。
　　（4）該方案對裝置采樣率和通訊速率沒有過高的要求，能夠在現有技術條件下實現，具有較高的實用價值。

      超(特)高壓輸電長線中為吸收高壓電網過剩的無功功率，防止過電壓，同時對線路進行參數補償，通常需要裝設并聯電抗器。并聯電抗器可能裝設在線路兩側，也可能裝設在線路中間，或線路兩側和中點均裝設。行波傳輸到并聯電抗器時，會發生反射和折射，即使線路內部無故障時，兩側方向性行波的差值也會產生不平衡電流，大大抬高動作門檻值，影響行波差動保護的靈敏度，因此有必要采取措施消除并聯電抗器的影響。